طراحی مدارهای حسابی با استفاده از Verilog
در شکل ۹ یک جدول صحت مربوط به یک تمام جمع کننده با سه ورودی x و y و cin و خروجیهای s و cout را مشاهده میکنید. برای رسم این مدار ابتدا به نقشه کارنو نیاز داریم (شکل ۱۰). مدار نهایی این تمام جمع کننده در شکل ۱۱ نمایش داده شده است.
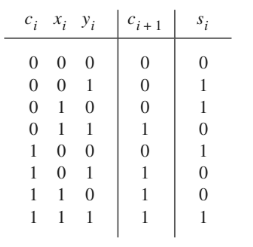 شکل ۹
شکل ۹ 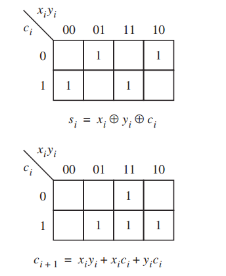 شکل ۱۰
شکل ۱۰
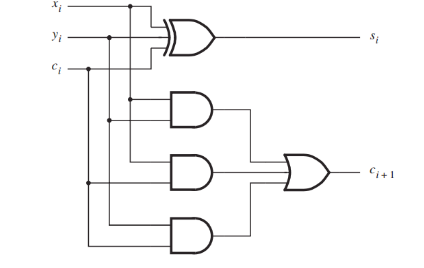 شکل ۱۱
شکل ۱۱
بک روش برای توصیف این مدار با استفاده ازVerilog، مدل سازی در سطح گیت است که در شکل ۱۲ مشخص شده است.
 شکل ۱۲
شکل ۱۲
روش دیگر برای توصیف این مدار استفاده از عبارات منطقی به روش مقدار دهی مداوم است که در شکل ۱۳ مشاهده میکنید. در این روش بجای عملگر XOR از علامت «^» استفاده شده است.
 شکل ۱۳
شکل ۱۳
حال میتوان یک تمام جمع کننده ۴ بیتی را با استفاده از ماژول ساخته شده تولید نمود.برای این کار نیاز به استفاده از چهار تمام جمع کننده ۱ بیتی(به عنوانsubcircuit) در مدار داریم که تمام آنها باید به هم متصل شوند. عدد اول با استفاده از چهار سیگنال x1، x2، x3 و x4 و عدد دوم با استفاده چهار سیگنال y0، y1، y2 و y3 مشخص شدهاند. حاصل جمع مدار به صورت s0، s1، s2 و s4 نمایش داده شده است. بیت ورودی نقلی مدار بصورت carryin برای کم ارزشترین بیت و خروجی نقلی مدار بصورت carryout برای آخرین بیت (پر ارزش ترین بیت) مدار مشخص شده است.
برای توصیف مدار جمع کننده ۴ بیتی در شکل ۱۴ از چهار عبارت برای نمونه سازی از ماژول fulladd استفاده شده است. هر کدام از این عبارتها با همین اسم شروع میشوند.پس از آن نام نمونه میآید. سپس نام سیگنال هایی که باید در ماژول fulladd استفاده شوند ذکر میگردد. نام این سیگنال ها باید به همان ترتیبی که در ماژول fulladd آمده است، در نمونه سازی قید شود.
نام سیگنال های موجود در هر نمونه، بیان میکند که چگونه تمام ۴ جمع کننده به هم متصل هستند. برای مثال بیت خروجی نقلی نمونه stage0 به بیت ورودی نقلی نمونه stage1 متصل شده است. ماژول fulladd و adder4 را میتوان در یک فایل Verilog نوشت. همچنین این دو ماژول را میتوان در دو فایل جدا تعریف کرد؛ که در این حالت باید مکان فایل fulladd را به کامپایلر معرفی نمود.
 شکل ۱۴
شکل ۱۴